分散化的威力
发布时间:2021-1-14 15:08阅读:1304
分散化的威力
7.1节介绍了分散化的理念,但是由于系统风险的存在,分散化带来的益处存在限制。有了前面的工具,我们可以重新考虑这一问题,同时深入窥探分散化的威力。
回忆式(7-16),组合的方差为
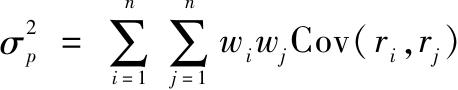
考虑最简单的分散化策略,组合中每一资产都是等权重的,即w i =1/n,这时式(7-16)可写作(将i=j的情况从连加符号中移出, 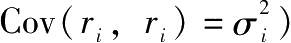
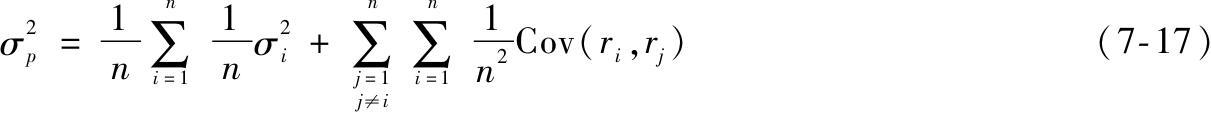
定义平均方差和平均协方差为
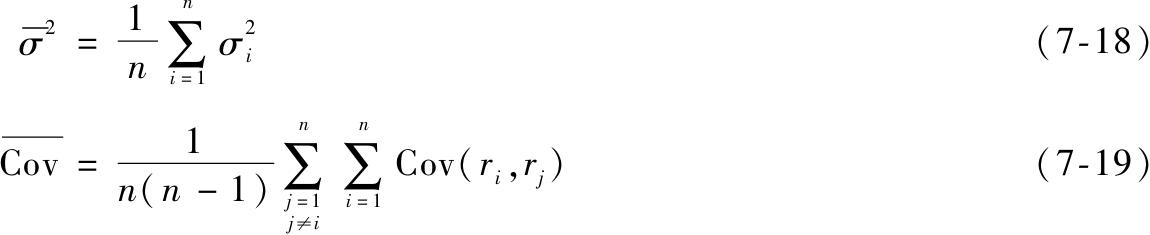
得出组合的方差为

现在检验分散化的效果。当证券之间的平均协方差为零时,即所有风险都是公司特有的,由式(7-20)可知组合方差在n变大时趋近于零。因此,当证券间收益不相关时,分散化降低组合风险的威力是无穷的。
然而,更重要的是,经济层面的风险因素使股票收益存在正相关性。在这种情况下,当组合高度分散化后,组合方差为正。当n变大时,尽管公司特有的风险最终被消除了,但是等号右边第二部分趋于Cov。因此分散化组合不可消除的风险取决于不同证券间收益率的协方差,这反过来就是经济中系统性因素的显现。
为了进一步考察系统风险和各证券间相关性的关系,简单假设所有证券的标准差都为σ,证券间相关系数都为ρ,协方差为ρσ 2 ,此时式(7-20)化为

证券间相关性的影响这时就很明显了。当ρ=0时,我们得到保险原理,组合方差在n变大时趋于零。然而,当ρ>0时,组合方差为正。实际上,当ρ=1时,不论n如何,组合方差等于σ 2 ,说明分散化没有意义。在完全相关的情况下,所有风险都是系统的。更一般的情况,当n增大,系统性风险保持为ρσ 2 。
表7-4给出了证券数量扩大时ρ=0,ρ=0.4两种情况下的组合标准差。其中令σ=50%。正如我们预想的,组合风险在ρ=0.4时更大。更令人吃惊的是,相关系数为正时,组合风险随着证券数量上升而下降的速度相对慢很多,因为证券间的相关性限制了分散化的空间。
表7-4 相关性和无相关性的证券等权重构造组合的风险减少
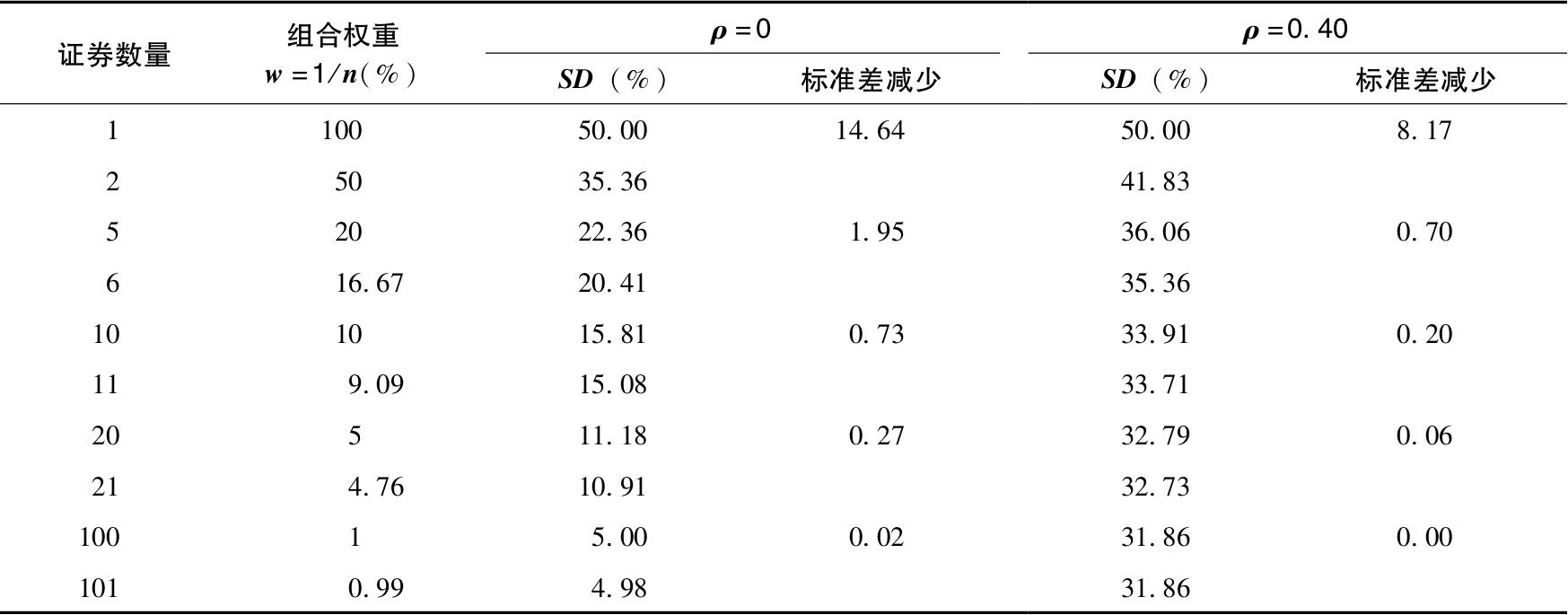
注意到对100个证券构成的组合,彼此不相关的情况下标准差为5%,和零标准差还有一段距离。当ρ=0.40,标准差很高,达到31.86%,非常接近于不可分散的系统性风险,为 
 ,说明进一步分散化也没什么意义了。
,说明进一步分散化也没什么意义了。
上面计算中最重要的一点是:当我们持有分散化组合时,某一证券对于整个组合风险的贡献取决于该证券和其他证券之间的协方差,并非该证券的方差。在第9章我们将会看到,这意味着风险溢价也取决于协方差而非收益的变动。
温馨提示:投资有风险,选择需谨慎。


 问一问
问一问
 +微信
+微信
 分享该文章
分享该文章












