预期尾部损失

当我们通过观测最坏的5%的情况来评估尾部风险时，VaR是所有这些情况中收益率最高（损失最小）的。一个对损失敞口头寸更加现实的观点是：关注最坏情况发生条件下的预期损失。这样的一个值有两个名称： 预期损失 （expected shortfall，ES） 或 条件尾部期望 （conditional tail expectation，CTE） ，后者强调了其与左尾分布之间的密切关系。在本书中，我们使用预期损失这一名称。

我们对前一节VaR的例子进行拓展，我们假设每一个样本点发生的概率相同。因此，我们需要求最底部的5%的观测的平均值。和前面的插值过程一样，我们给最底部的4个值的权重为4/4.2，而给第5个值的权重为0.2/4.2，这样可以求得ES=-35.94%，显著小于VaR的值-25.56%。

（注：Jonathan Treussard给出了正态分布下ES的一个公式（见“The Nonmonotonicity of Value-at-Risk and the Validity of Risk Measures over Different Horizons”，IFCAI Journal of Financial Risk Management，March 2007）。其公式为

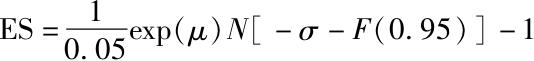
其中μ为连续复利计算的收益率的均值，σ是其标准差，N（·）为标准正态分布的累计分布函数，F是其逆函数。在上面的例子中，μ和σ的估计值分别为5.47%和19.54%。正态分布假设下，我们有ES=-30.57%，这表明这一分布相比于正态分布有更大的左尾值。需要注意的是，虽然VaR和ES都是利用历史样本估计的无偏估计值，但是仍然可能包含很大的估计误差。）