两个风险资产的组合
发布时间:2021-1-14 14:59阅读:8153
两个风险资产的组合
在上一部分我们考查了多个证券等权重构造组合的分散化问题,现在是研究有效分散化的时候了,给定任何期望收益我们可以构造最低风险的风险资产组合。
两个风险资产构成的组合相对容易分析,其原理也可应用于多个资产组合。所以我们讨论两个资产(一个专门投资长期债券的基金D,一个专门投资股票的基金E)构成的资产配置。表7-1列出了这两个基金的收益分布。
投资于债券基金的比例定义为w D ,剩余的1-w D ,定义为w E ,投资于股票基金。这个组合的收益率r p 是 
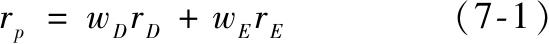
表7-1 两个共同基金的描述性统计

r D 和r E 分别是债券基金和股票基金的收益率。
组合的期望收益是两种证券期望收益的加权平均值,权重分别为其投资的比例
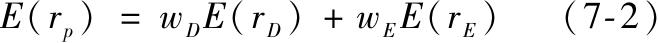
方差是
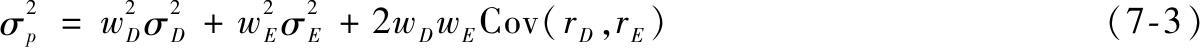
可以看出组合的方差并不像期望收益率,并不是两个基金方差的加权平均。为了更好地理解组合方差,回想一个变量和它自己的协方差就是这个变量的方差
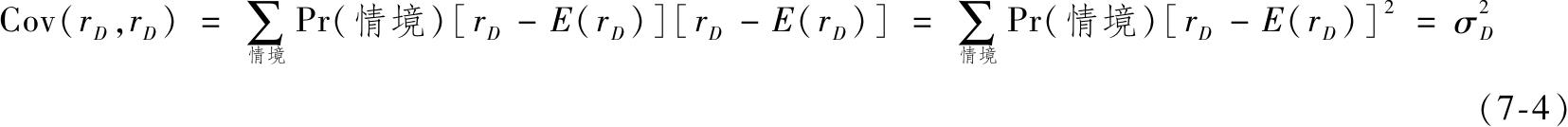
因此,组合方差的另一种表达方式为
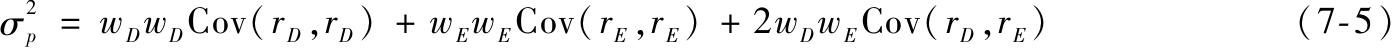
组合方差就是协方差的加权值,权重为协方差内一对资产在组合中权重的乘积。
表7-2展示如何用数据表计算组合的方差。表7-2a分别给出了两只基金收益的协方差矩阵。
表7-2 组合方差的计算

根据基金占投资组合权重形成的协方差矩阵,不同权重比例标注在矩阵的外沿,即第一行和列。投资组合方差等于协方差矩阵中的每个元素与不同行列对应的权重交乘,再将各项相加,便得到了公式7.5给出的投资组合方差。
表7-2b展示了这一计算过程,即交乘协方差矩阵:每个协方差同时乘以行和列中的外围权重。表7-2b最后一栏将所有协方差项进行加总,得到了与投资组合方差方程7.5一样的计算结果。
计算过程中,由于协方差矩阵是关于对角线对称的,即  ,因此,每个协方差项出现两次。
,因此,每个协方差项出现两次。
交乘协方差矩阵可应用于多项资产组合方差的计算。表格方式以简单的实现这一计算过程。概念检查1要求你尝试计算三项资产组合的方差。通过这个练习来考察你对这个概念是否深刻理解。
式(7-3)揭示了如果协方差为负,那么组合的方差会降低。但即使协方差为正,组合标准差仍然低于两个证券标准差的加权平均,除非两个证券是完全正相关的。
概念检查7-1a.验证上面协方差计算方法和式(7-3)是一致的。
b.考虑三个基金X、Y和Z,权重为w X 、w Y 和w Z 。证明组合方差是
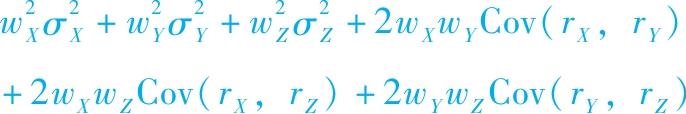
为了证明这一点,注意到协方差可由相关系数ρ DE 计算得到
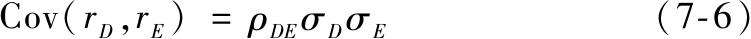
因此
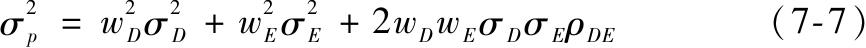
其他不变,当ρ DE 高时组合方差就高。当两个资产完全正相关,即ρ DE =1时,等号右边可化简为
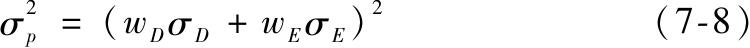
或

因此,组合标准差就是两个收益完全正相关资产标准差的加权平均。在其他情况下,相关系数小于1,使得组合标准差小于两个资产标准差的加权平均。
一个对冲资产和组合中的其他资产相关性为负。由式(7-7)可知这类资产在减少组合总风险上特别有效,而且,式(7-2)显示期望收益并不受相关性影响。因此,其他条件不变,我们总是愿意在组合中增加与组合相关性小甚至负相关的资产。
因为组合期望收益率是各个资产期望收益的加权值,而标准差小于各个资产标准差的加权平均,所以非完全正相关的资产组合在一起总是比单个资产提供更好的风险-收益机会。资产相关性越小,有效收益越大。
组合的标准差最低是多少呢?最低的相关系数是-1,代表完全负相关。在这种情况下,式(7-7)简化为

组合标准差为

当ρ=-1时,通过解下式可以得到完全对冲的头寸
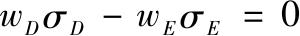
解为

这一权重使得组合标准差变为零。
【例7-1】组合的风险和收益让我们把这一分析方法应用于表7-1中的债券和股票基金中。用这些数据,组合期望收益、方差和标准差的方程为:
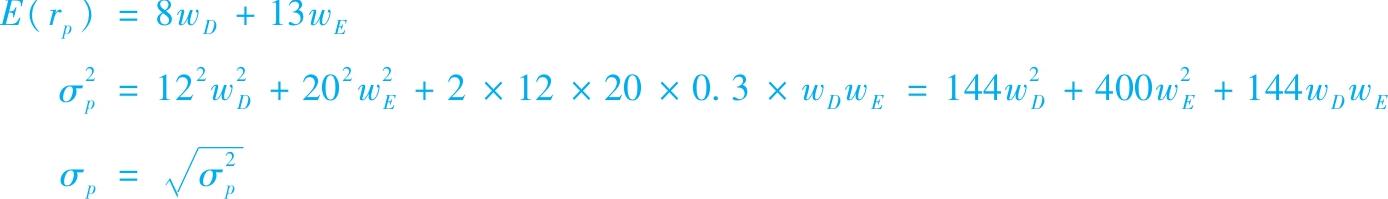
我们可以变化组合的成分比例来看整个组合期望收益和方差的变化。假设改变债券的比例,组合期望收益如表7-3和图7-3所示,当债券比例从0变到1时,组合期望收益从13%降到8%。
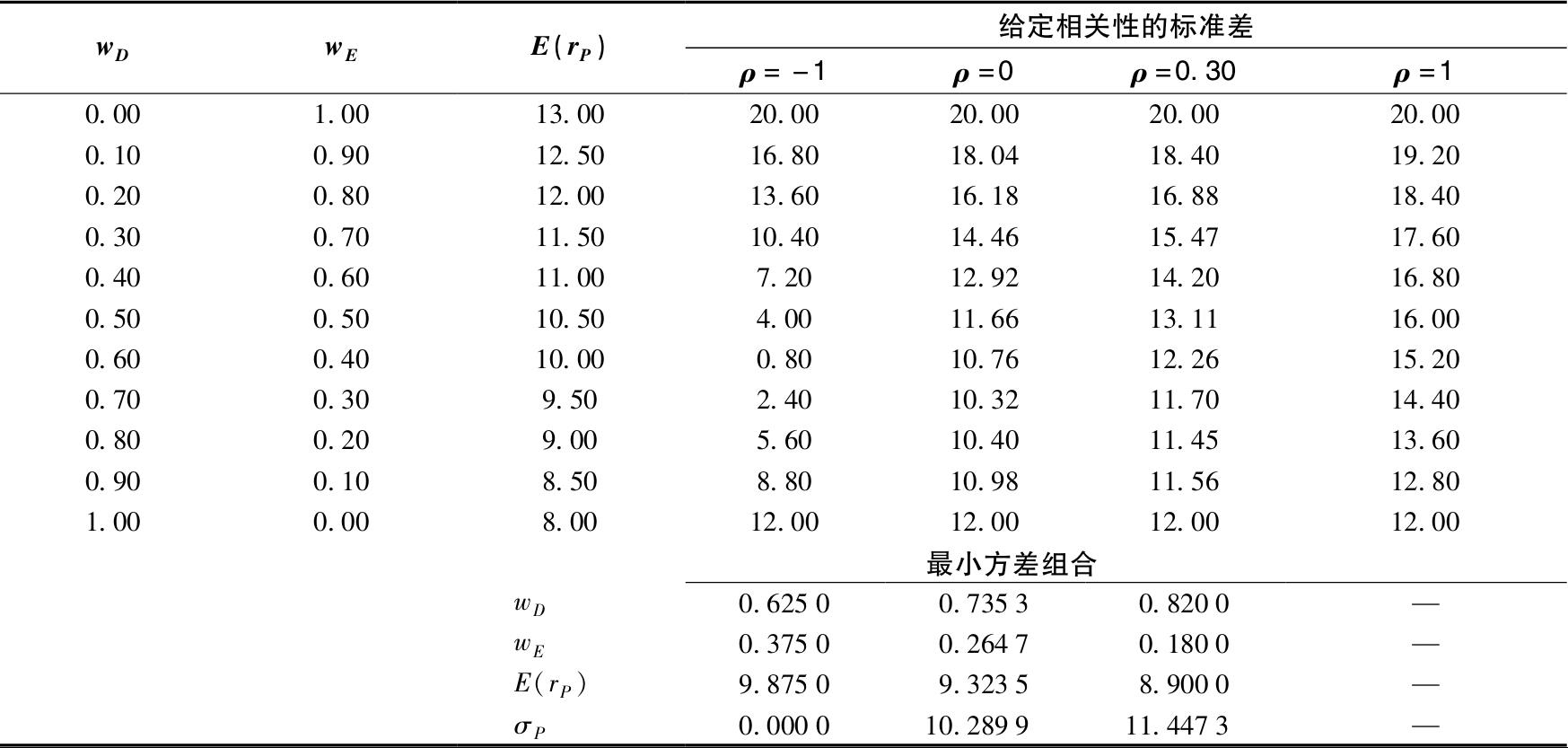
表7-3 不同相关系数下的期望收益和标准差
当w D >0,w E >1时情况如何呢?这种情况的组合策略是卖空股票基金并将资金投于债券基金。这将会继续降低组合的期望收益率。例如,当w D =2,w E =-1时,预期组合收益降到2×8+(-1)×13=3%,此时的债券基金规模是组合净值的两倍。
相反的情况是w D <0,w E >1时,这种策略需要卖空债券基金来筹资购买股权基金。
当然,不同的投资比例对组合的标准差也有影响。表7-3展示了假设不同的相关系数根据式(7-7)计算的不同组合权重时的组合标准差。图7-4显示了组合标准差和两个基金权重的关系。先看ρ DE =0.3,图像显示当股票投资比例从0到1,组合的标准差先降后升。只要在相关性不是很高的情况下都是如此。当两个基金的正相关性非常高时,组合的标准差随着组合由低风险向高风险资产转移而上升。
(注:只要  ,当我们从全部投资与债券开始逐渐增加股权投资时,波动率将先下降。)
,当我们从全部投资与债券开始逐渐增加股权投资时,波动率将先下降。)
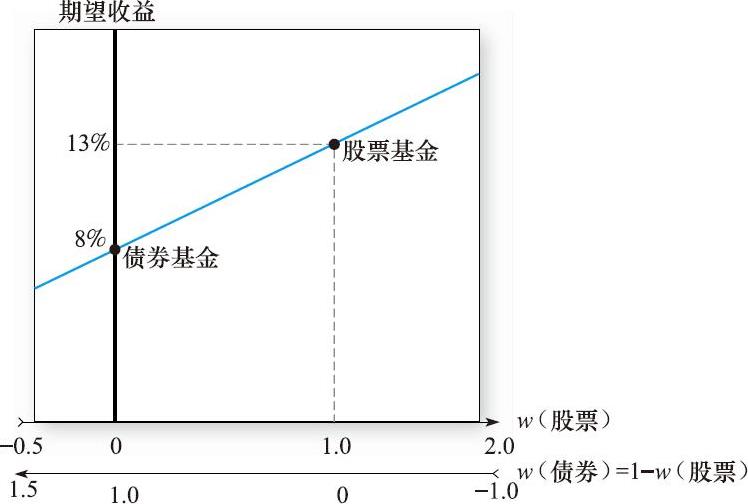
图7-3 组合期望收益关于投资比例的函数
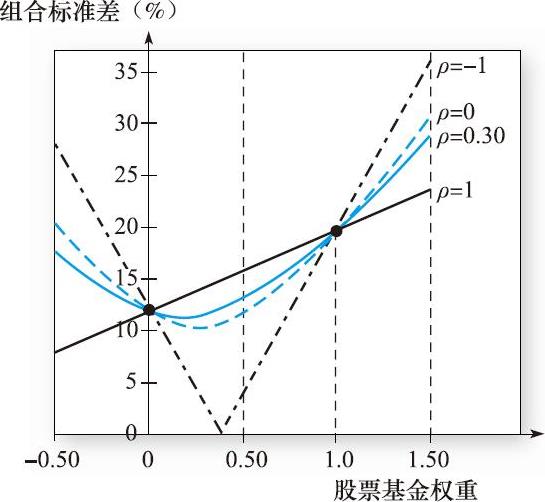
图7-4 组合标准差关于投资比例的函数
那么组合标准差最低是多少呢?对于表7-1中的数据来说,这一最小化问题的解是
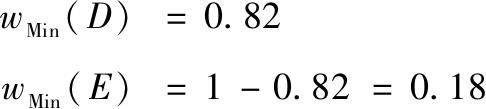
(注:这一解法利用了微积分中求极小值的方法。运用式(7-3)写出资产组合方差的表达式,用1-w D 代替w E ,并对w D 求微分,利用导数为零来求解w D 可以得到
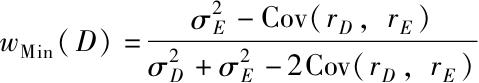
同样,利用Excel软件中的表单程序Solver来求解方差极小化问题,你可以获得一个精确的解。附录7A给出了资产组合和优化的一个实例。)
组合标准差是
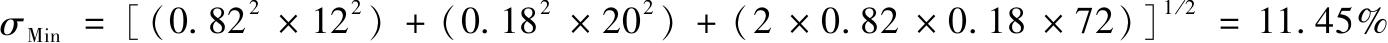
即表7-3中ρ=0.30一列的最后一行σ p 值。
图7-4中ρ=0.3的线经过两个未经分散化的点,w D =1和w E =1。注意到 最小方差组合 (minimum-variance portfolio) 的标准差小于这两个点的标准差。这显示了分散化的效果。
图7-4中另外3条曲线表示:保持每个资产方差不变时,组合的风险因两个资产收益相关系数变化而变化,这3条曲线对应着表7-3中的3列内容。
连接了W D =1全债券组合和W E =1全股票组合的黑色实线给出了ρ=1完全正相关资产构成组合的标准差,这种情况下分散化是没有意义的,组合标准差不过是两个标准差的加权平均。
浅色虚线给出了彼此不相关的资产(ρ=0)构成的组合风险情况。资产相关性越小,分散化则更加有效,组合风险也越低(至少当两资产都是多头头寸时)。ρ=0的最小组合标准差是10.29%,低于任意一个资产的标准差。
最后,折线说明了当两资产完全负相关(ρ=-1)时可以完全对冲的情况。这时最小方差组合的解由式(7-12)给出
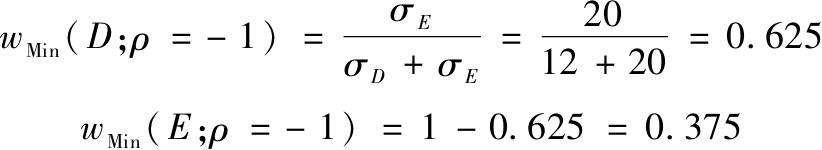
组合方差为0。
我们可以组合图7-3和图7-4来展示组合风险与期望收益的关系。对于任意一对投资比例w D ,w E ,我们从图7-3中得到期望收益,从图7-4中得到标准差。表7-3中每对期望收益率和标准差的结果如图7-5所示。
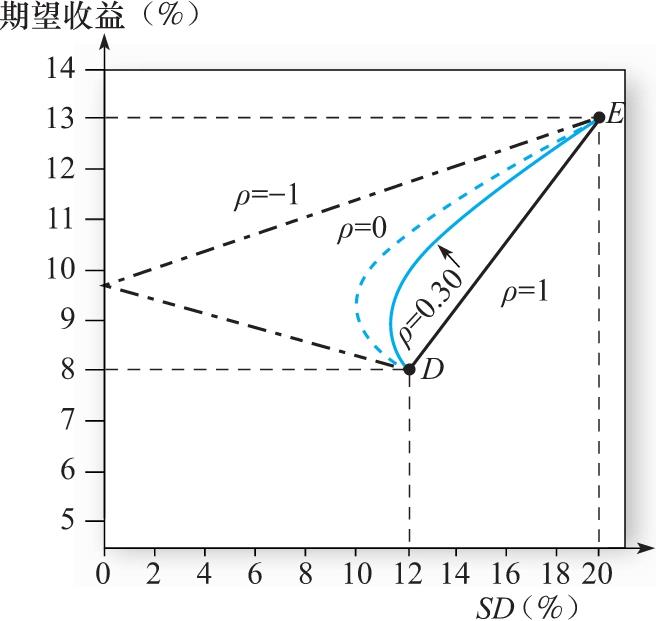
图7-5 组合期望收益关于标准差的函数
图7-5中的浅色实线说明ρ=0.3的 投资组合可行集 (portfolio opportunity set) 。我们之所以称其为投资组合可行集,是因为它表示了两个资产构造的所有期望收益和标准差的组合。其他的曲线表示了不同相关系数下的情况。黑色实线说明完全正相关的资产分散化并没有意义。曲线说明分散化是有意义的。当ρ=-1时,投资组合可行集是线性的,但是它提供了完全对冲的机会最大化了分散化的好处。
总之,尽管任何组合的期望收益是几个资产期望收益的加权平均,但标准差并不是这样。当资产相关系数小于1时分散化可以带来好处,且相关性越低,好处越大。在完全负相关的情况下,存在完美的对冲机会来构造零方差组合。
概念检查7-2计算并画出当债券和股票基金相关性为0.25时的投资组合可行集。
假设一个投资者想要从可行集中选择最优组合,他需要考虑风险厌恶。图7-5右上方的组合期望收益较高但是风险敞口也高。最优点取决于个人偏好。风险厌恶程度更高的投资者偏好于左下角期望收益低但是风险也相对较低的组合。
(注:给定风险厌恶水平,个人可以决定提供最高效用值的组合。在第6章我们可以用关于期望收益和标准差的效用公式来描述效用值。组合的期望收益和标准差由两个资产在组合中的权重决定。根据式(7-2)和式(7-3),得
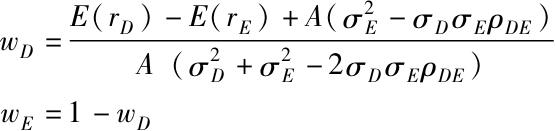
同样,可以利用Excel的Solver程序,以式(7-2)、式(7-3)以及W D +W E =1(即所有权重之和为1)为约束条件来最大化效用函数。)
温馨提示:投资有风险,选择需谨慎。
 今天有两个新股可以申购吗?是哪两个?
今天有两个新股可以申购吗?是哪两个?


 问一问
问一问
 +微信
+微信
 分享该文章
分享该文章












